Coronavirus news #3. Just one point today, but it's an important (and loooong) one. Summary at bottom if you want to skip. As usual, I welcome pushback.
COVID-19 models have been in the news lately and there is a brewing fight over whether to believe models - and consequently, scientists. This fight is going to have enormous political and social consequences for billions. But there is a lot of confusion about models in general. This is an area I know a bit about, so I'm going to try to briefly explain how they work. And while I will continue to stick up for epidemiological modelling efforts, I'm now worried about the hugely influential IHME model and will explain why.
Unfortunately, scientists use the term 'model' to mean a huge range of things. We confuse each other when we don't specify what we mean further; I can't tell you how common it is in my field to stop someone and ask "What kind of model are you talking about?". Here are 3 types of model that are relevant to this discussion (note: this is just a simple shorthand I came up with for this post, it's not some actual classification):
1) I plot some data on a graph and use some algorithm to draw a straight or curved line through the data. The line - or its mathematical description - is a model. If I want to predict/forecast what will happen outside the range of the data (e.g. in the future, if time is on your X axis), I just extend the line on the graph.
2) I expect to see a particular shape (e.g. a 'U' shape) either because I've seen data on a similar topic before or it seems logical. When I get new data, I plot it and then draw that same 'U' line over the new data. It can be stretched or squashed to 'fit' the new data but it will still be a U. The U line is a model. If I want to predict/forecast outside the range of the data, I can again extend the 'fitted' line on the graph.
3) I write a mathematical description of how a system works (a 'system' can be essentially anything that changes). This takes the form of a set of equations that capture the logic of the system. These equations jointly form a model. You can 'fit' these equations to data to understand a specific example of the system, or you can keep it abstract to understand how they work in general. If I want to predict/forecast what will happen in a specific example, I can no longer just extend a line. Instead, I must solve the equations to understand what will happen.
You can see that there is increasing complexity/sophistication in these three types of models. They all have their place, and I use all three in my work. In some situations a complex model will give you the same answer as a simple one, but the complex model will involve a lot more work and error-checking, so we go with a type 1 or type 2. But these can fail badly in some situations, especially when you are using them to predict/forecast outside the range of the data. For some common shapes, they will predict infinity or negative infinity if you extend your predictions far enough, which makes no sense. Type 3 is much more robust to this because it is built on and constrained by the logic of the system. However, they can also predict garbage if your equations are wrong i.e. you have not captured the logic correctly. A lot of time is spent thinking about ways to diagnose the model to make sure that the equations are correct (and consequently, the predictions reliable). In general, type 3 is more reliable to predict the future, and much of our world is based on science and technology built on this type of model.
Now about COVID-19.
All three types of models are currently being used, with little discussion about the assumptions, strengths and weaknesses. There are many sophisticated models out there (see a list at https://docs.google.com/.../1hUZlVDPfa5C8KgURoP.../edit...), though they are hobbled by poor data to feed into them. But at present, the US political and healthcare systems are making plans that are heavily reliant on the IHME model. You can read the model description here (https://www.medrxiv.org/.../2020.03.27.20043752v1.full.pdf). It is mostly type 2, and in my opinion (and more importantly, that of several epidemiologists) they make some large and worrisome assumptions.
The big one is that the type 2 'shape' that they rely on is entirely based on official data from Wuhan. Why is this a problem?(i) We don't fully know how reliable that data is. Data from Italy and Spain are thought to be off by a factor of 2, for reference, and I expect most people have even less faith in China's official numbers. [EDIT: Laura points out that the model has been recently updated to include data from Spain and Italy. That data is biased too so it does not fix the problem, but it is probably improves things.] (ii) It seems to assume that lockdown measures in the US will have the same effect that they did in China. But China implemented a lockdown that is far more strict that anything envisaged by Europe or North America; I doubt that most countries would tolerate anything comparable. Both of these issues point towards the direction of the model predictions being far too optimistic. As a consequence, their predictions of when the epidemic will peak and when it will end do not seem reliable.
All models make assumptions and have weaknesses, so how do we diagnose whether a model's predictions are good? That's a really complex topic! Epidemic models are not like weather models. Nothing we do affects the weather in the short term, so we can just evaluate how the weather played out after a prediction is made. But we change our behaviour and policies based on epidemic models, which makes important model assumptions wrong; our actions therefore make the predictions less likely to come true. So when the predictions fail, it could be either because of the change we made, or because the model was not good, and it's hard to distinguish those.
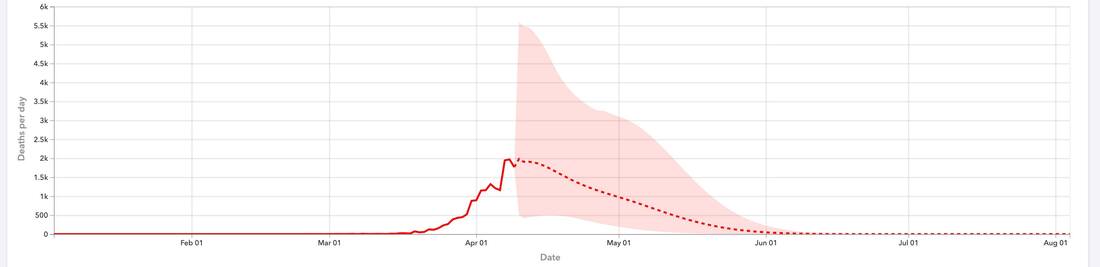
This post is long enough, so let's take a look at one graph that indicates that the IHME predictions are a bit questionable. The attached graph from the IHME website shows the number of deaths per day till April 10th and their forecasts thereafter. The shaded area indicates the model uncertainty; roughly speaking, the range of possible values. You will see that the uncertainty is highest immediately after the data stops and then decreases steadily afterwards. This is rather strange; do we really know much less about how many people will die tomorrow than about how many people will die 2 weeks from now? Our uncertainty should generally increase as we look into the future (at least for some time - if you look far enough ahead, uncertainty will decline because the pandemic will end). To me, this suggests that something may be wrong under the hood; the 'shape' is wrong in an important way. The alternative is that this is a case of poor data visualisation.
Bottom line: if you're in the US, be at least mildly sceptical about the official predictions about number of deaths at this point, since many seem to be based off a model whose assumptions are hard to justify. The predictions about the date of the peak seem even less reliable. The model projections could still end up being correct, but I'm not very confident in it and would prefer to rely on a model that includes mechanisms (a type 3 model, of which there are several out there) rather than questionable statistical relationships.
I would like to reiterate that we absolutely need to rely on models to make these kinds of predictions, and epidemiology is a sophisticated science - we are not stumbling in the dark here. But we can and should evaluate individual models critically, especially when they are guiding important policies.
COVID-19 models have been in the news lately and there is a brewing fight over whether to believe models - and consequently, scientists. This fight is going to have enormous political and social consequences for billions. But there is a lot of confusion about models in general. This is an area I know a bit about, so I'm going to try to briefly explain how they work. And while I will continue to stick up for epidemiological modelling efforts, I'm now worried about the hugely influential IHME model and will explain why.
Unfortunately, scientists use the term 'model' to mean a huge range of things. We confuse each other when we don't specify what we mean further; I can't tell you how common it is in my field to stop someone and ask "What kind of model are you talking about?". Here are 3 types of model that are relevant to this discussion (note: this is just a simple shorthand I came up with for this post, it's not some actual classification):
1) I plot some data on a graph and use some algorithm to draw a straight or curved line through the data. The line - or its mathematical description - is a model. If I want to predict/forecast what will happen outside the range of the data (e.g. in the future, if time is on your X axis), I just extend the line on the graph.
2) I expect to see a particular shape (e.g. a 'U' shape) either because I've seen data on a similar topic before or it seems logical. When I get new data, I plot it and then draw that same 'U' line over the new data. It can be stretched or squashed to 'fit' the new data but it will still be a U. The U line is a model. If I want to predict/forecast outside the range of the data, I can again extend the 'fitted' line on the graph.
3) I write a mathematical description of how a system works (a 'system' can be essentially anything that changes). This takes the form of a set of equations that capture the logic of the system. These equations jointly form a model. You can 'fit' these equations to data to understand a specific example of the system, or you can keep it abstract to understand how they work in general. If I want to predict/forecast what will happen in a specific example, I can no longer just extend a line. Instead, I must solve the equations to understand what will happen.
You can see that there is increasing complexity/sophistication in these three types of models. They all have their place, and I use all three in my work. In some situations a complex model will give you the same answer as a simple one, but the complex model will involve a lot more work and error-checking, so we go with a type 1 or type 2. But these can fail badly in some situations, especially when you are using them to predict/forecast outside the range of the data. For some common shapes, they will predict infinity or negative infinity if you extend your predictions far enough, which makes no sense. Type 3 is much more robust to this because it is built on and constrained by the logic of the system. However, they can also predict garbage if your equations are wrong i.e. you have not captured the logic correctly. A lot of time is spent thinking about ways to diagnose the model to make sure that the equations are correct (and consequently, the predictions reliable). In general, type 3 is more reliable to predict the future, and much of our world is based on science and technology built on this type of model.
Now about COVID-19.
All three types of models are currently being used, with little discussion about the assumptions, strengths and weaknesses. There are many sophisticated models out there (see a list at https://docs.google.com/.../1hUZlVDPfa5C8KgURoP.../edit...), though they are hobbled by poor data to feed into them. But at present, the US political and healthcare systems are making plans that are heavily reliant on the IHME model. You can read the model description here (https://www.medrxiv.org/.../2020.03.27.20043752v1.full.pdf). It is mostly type 2, and in my opinion (and more importantly, that of several epidemiologists) they make some large and worrisome assumptions.
The big one is that the type 2 'shape' that they rely on is entirely based on official data from Wuhan. Why is this a problem?(i) We don't fully know how reliable that data is. Data from Italy and Spain are thought to be off by a factor of 2, for reference, and I expect most people have even less faith in China's official numbers. [EDIT: Laura points out that the model has been recently updated to include data from Spain and Italy. That data is biased too so it does not fix the problem, but it is probably improves things.] (ii) It seems to assume that lockdown measures in the US will have the same effect that they did in China. But China implemented a lockdown that is far more strict that anything envisaged by Europe or North America; I doubt that most countries would tolerate anything comparable. Both of these issues point towards the direction of the model predictions being far too optimistic. As a consequence, their predictions of when the epidemic will peak and when it will end do not seem reliable.
All models make assumptions and have weaknesses, so how do we diagnose whether a model's predictions are good? That's a really complex topic! Epidemic models are not like weather models. Nothing we do affects the weather in the short term, so we can just evaluate how the weather played out after a prediction is made. But we change our behaviour and policies based on epidemic models, which makes important model assumptions wrong; our actions therefore make the predictions less likely to come true. So when the predictions fail, it could be either because of the change we made, or because the model was not good, and it's hard to distinguish those.
This post is long enough, so let's take a look at one graph that indicates that the IHME predictions are a bit questionable. The attached graph from the IHME website shows the number of deaths per day till April 10th and their forecasts thereafter. The shaded area indicates the model uncertainty; roughly speaking, the range of possible values. You will see that the uncertainty is highest immediately after the data stops and then decreases steadily afterwards. This is rather strange; do we really know much less about how many people will die tomorrow than about how many people will die 2 weeks from now? Our uncertainty should generally increase as we look into the future (at least for some time - if you look far enough ahead, uncertainty will decline because the pandemic will end). To me, this suggests that something may be wrong under the hood; the 'shape' is wrong in an important way. The alternative is that this is a case of poor data visualisation.
Bottom line: if you're in the US, be at least mildly sceptical about the official predictions about number of deaths at this point, since many seem to be based off a model whose assumptions are hard to justify. The predictions about the date of the peak seem even less reliable. The model projections could still end up being correct, but I'm not very confident in it and would prefer to rely on a model that includes mechanisms (a type 3 model, of which there are several out there) rather than questionable statistical relationships.
I would like to reiterate that we absolutely need to rely on models to make these kinds of predictions, and epidemiology is a sophisticated science - we are not stumbling in the dark here. But we can and should evaluate individual models critically, especially when they are guiding important policies.
